Concepto de derivada con Geogebra
Concepto de Derivada utilizando Geogebra
En el primer ejemplo, presenta la función ![]() , y moviendo los puntos, se puede observar cómo cambia la recta tangente, y la recta secante, tanto gráficamente como numéricamente, calculando sus pendientes. A continuación se hacen unas preguntas cuyas respuestas pueden ayudar a comprender el concepto de derivada como límite de las pendientes de las rectas secantes.
, y moviendo los puntos, se puede observar cómo cambia la recta tangente, y la recta secante, tanto gráficamente como numéricamente, calculando sus pendientes. A continuación se hacen unas preguntas cuyas respuestas pueden ayudar a comprender el concepto de derivada como límite de las pendientes de las rectas secantes.
En un segundo ejemplo, hace lo mismo, pero con la función 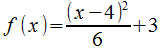
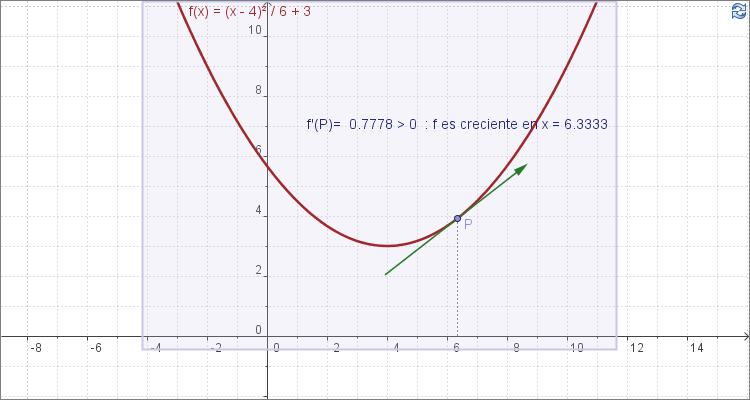
A continuación para visualizar la relación de la derivada con el crecimiento y decrecimiento, al mover el punto sobre la gráfica de la función lo que se observa es el vector tangente en cada punto, la pendiente y nos indica si la función es creciente o decreciente.
Vuelve a utilizar los mismo ejemplos que en el caso anterior en un primer ejemplo la función ![]() , y en un segundo ejemplo
, y en un segundo ejemplo 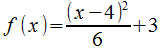
Una tercera etapa que nos ayudaría con el concepto de devivada sería el estudio de la función derivda, en este caso, para cada punto que elijamos sobre la gráfica de la función nos dibujaría otro punto cuya abscisa es la misma y cuya ordenada es la derivada de la función en ese punto, de esa forma, al ir moviendo el punto sobre la gráfica de la función va apareciendo la función derivada. Para el cálculo de la derivada en cada punto, nos dibuja, partiendo del punto la recta tangente, y un triángulo sobre ella cuyo cateto horizontal mide uno, y por lo tanto la derivada sería la medida del cateto vertical.
Las funciones utilizadas son, para el primer ejemplo, la función ![]() , para el segundo ejemplo
, para el segundo ejemplo 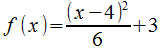 , e incluye un tercer ejemplo con la función
, e incluye un tercer ejemplo con la función ![]() .
.
Para terminar podemos encontrar las funciones derivadas de las principales funciones elementales, así tenemos
- La derivada de la función afín
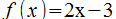 que sería una función constante
que sería una función constante - La derivada de la función cuadrática
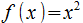 que es una función afín (lineal en este caso)
que es una función afín (lineal en este caso) - La dervada de una función exponencial
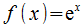 que es también una función exponencial (ella misma en este caso)
que es también una función exponencial (ella misma en este caso) - La derivada de una función logarítmica
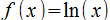 que es la función de proporcianalidad inversa
que es la función de proporcianalidad inversa

