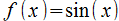
Concepto de Integral Definida

Escrito por Administrador en 13 de mayo de 2013. Publicado en Presentaciones.

 Integral Definida utilizando Geogebra

En el blog Mateguay de un grupo de profesores vascos, entre otras secciones, encontramos una dedicada a Geogebra.

Traemos aquí varias applets elaboradas por el profesor navarro Manuel Sada Allo, que nos ayudarán, con ejemplos, a explicar a nuestros alumnos el concepto de integral definida, como área que queda debajo de la gráfica de una función relacionandolo con las sumas inferiores y superiores de las áreas de las funciones escalonadas correspondientes.

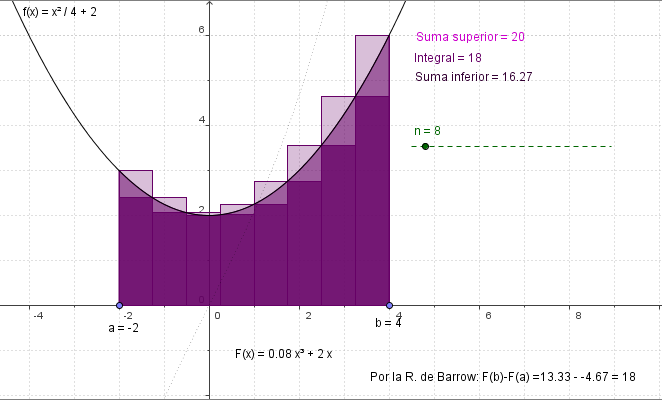
Para la función nos da una partición del intervalo, que podemos configurar con un deslizable, y nos representa y nos calcula el área de las dos funciones escalonadas correspondientes (la superior y la inferior) así como el área de la superficie que queda bajo la curva aplicando la Regla de Barrow.

Ovbiamente, al hacer más fina la partición se observa que la diferencia entre las áreas superior e inferior se va reduciendo, y por supuesto, el valor de la integral siempre queda en medio.

Aunque nos presenta un par de ejemplos con funciones concretas, simplemente haciendo clic con el botón derecho sobre la gráfica y eligiendo propiedades, se puede cambiar la expresión de la función representada.

A continuación se hacen unas preguntas cuyas respuestas pueden ayudar a comprender el concepto que trata de explicar.

Para explicar este concepto de integral definida como área que queda debajo de la gráfica de la función, utiliza un primer ejemplo: 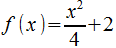, y un segundo ejemplo: .

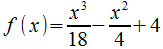A continuación introduce el Teorema Fundamental del cálculo, es decir a partir de una función va representando otra fución que nos da el área que queda debajo de la misma en un intervalo con extremo inferior fijo, y extremo superior variable, y como el programa, además de de dibujar esta función, calcula su expresión analítica, con lo que el alumno puede comprobar que al derivarla, obtiene la función inicial.

Para esto itruduce, también, tres ejemplos, el primer ejemplo con la función 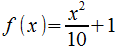, un segundo ejemplo con la función 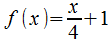e incluso un tercer ejemplo que sería la función