Mallas invisibles para recubrir el plano

Existen unas mallas invisibles que nos ayudan a recubrir el plano…

En ocasiones, las matemáticas nos proporcionan objetos invisibles que, aún sin verlos, nos pueden ayudar a realizar bonitas composiciones artísticas.

Vamos a ver el caso de los triángulos y los cuadriláteros. Aprenderemos a utilizarlos para hacer una composición que recubra el plano, y veremos cómo hacerlo, tanto con el ordenador como a mano, recortando las figuras y aprovechando para dar un nuevo uso a algunas revistas que ya no necesitemos.

Cuando cubrimos el plano utilizando figuras geométricas, decimos que estamos haciendo un teselado, o una teselación.

Recubrimos el plano con triángulos

{tab title=»Teorema de Napoleón» class=»blue»} 

El Teorema de Napoleón establece que, para cualquier triángulo, si construimos un triángulo equilátero sobre cada uno de sus lados y unimos los centros de esos triángulos equiláteros, obtenemos un nuevo triángulo equilátero. Aprovechando esta propiedad, podemos usar cualquier triángulo para hacer un bonito recubrimiento del plano.

En este enlace (clic aquí) tenemos una visualización con geogebra.

{tab title=»Lo hacemos a mano» class=»green»}

También podemos hacer la construcción «a mano». La composición se basa en repetir muchas veces el mismo triángulo. Para ello, podemos recortar muchos a la vez, por ejemplo reciclando las hojas de un folleto de publicidad o de una revista. El proceso podría ser el siguiente:

• Colocamos el primer triángulo.
• Tomando otros dos, los colocamos girándolos para que, entre los tres, dejen como hueco un triángulo equilátero.
• Vamos añadiéndo triángulos poco a poco siguiendo el procedimiento anterior, colocándolos de manera que siempre dejemos entre medias huecos que sean triángulos equilateros. ¡Cuidado! los triángulos siempre llevan la misma «orientación» (no debemos voltearlos).

{tab title=»Malla de triángulos equiláteros» class=»orange»}

• Si marcamos los centros de los tres triángulos equiláteros asociados a cualquiera de nuestros triángulos y los unimos, el Teorema de Napoleón nos dice que obtenemos un nuevo triángulo equilátero.
• Así que podemos marcar los centros de todos los triángulos equiláteros que teníamos (ver imágenes 1 y 2 de la composición), y realizar este proceso de creación de nuevos triángulos equiláteros.
• En la tercera imagen de esta composición, vemos cómo resultaría el primer triángulo equilátero, y en la cuarta, cómo ir realizando el proceso.

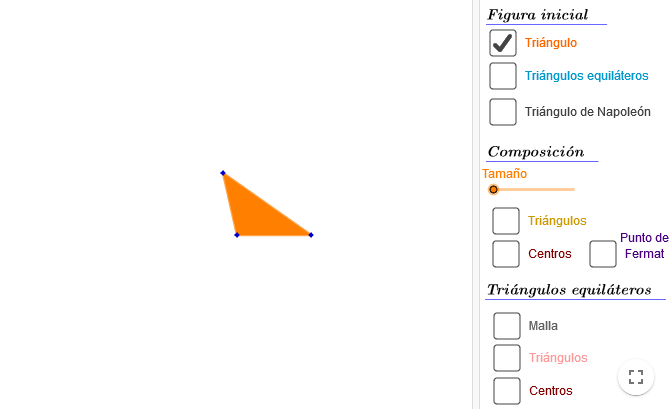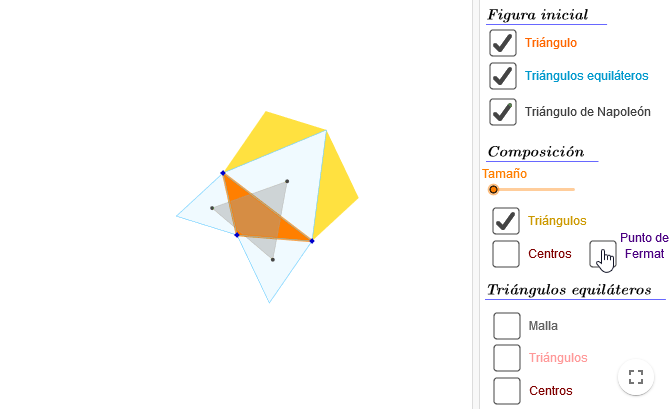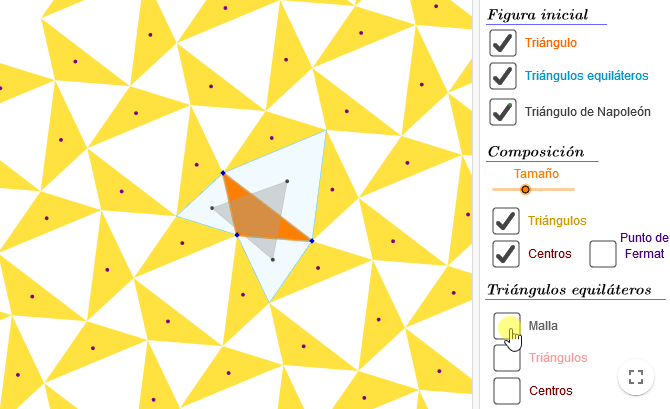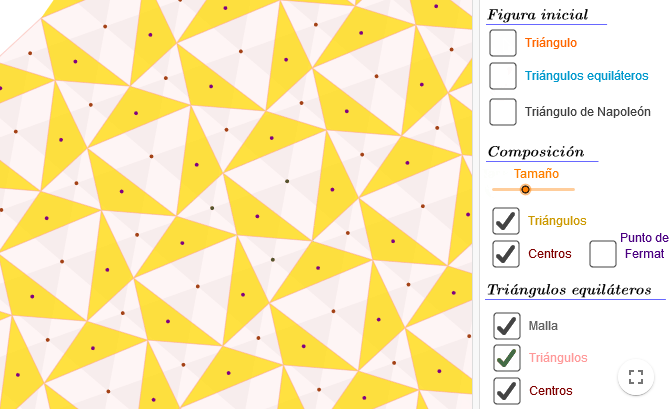
• Al dibujar todos los triángulos, habremos recubierto el plano con una bonita malla de triángulos equiláteros.

• Por último, podemos terminar nuestra composición artística marcando los centros de cada uno de estos nuevos triángulos equiláteros.

 

{tab title=»El punto de Fermat» class=»red»}

• Si nos fijamos en la construcción, una vez colocados los tres primeros triángulos, todo el recubrimiento puede obtenerse desplazando esa agrupación de tres triángulos.
• Las direcciones en las que hay podemos desplazarlos son cualquiera de las que unen cada vértice de los triángulos equiláteros con el otro vértice del triángulo inicial (activar la casilla «Punto de Fermat» para verlo).
• Los tres segmentos que definen esos desplazamientos tienen un punto en común. Es un punto notable del triángulo algo menos conocido, denominado punto de Fermat.

Cuando ninguno de los ángulos del triángulo original es menor que 120º, el punto de Fermat tiene la propiedad de que la distancia total a los vértices del triángulo es la mínima posible.

Esto lo hace particularmente interesante en situaciones muy reales. Podemos pensar en utilizarlo cuando tengamos que elegir un punto y la distancia a los vértices supondrá un coste económico o de tiempo.

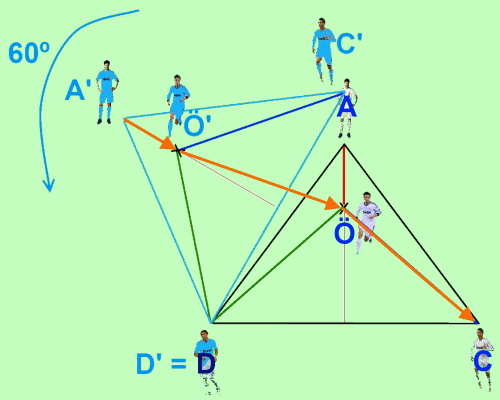
Por ejemplo, al construir el «tridge» de Midland, o al situar futbolistas en un campo de fútbol.

(Imagen de http://www.matifutbol.com/es/triangulo.html) 

{/tabs}

¿Te animas a hacer tu propia construcción? Recuerda que se puede con cualquier triángulo.

Recubrimos el plano con cuadriláteros

{tab title=»Una malla invisible» class=»blue»}

Una propiedad muy bonita de los cuadriláteros es que si unimos los puntos medios de los lados, ¡obtenemos un paralelogramo!
No importa cómo sea el cuadrilátero (incluso puede ser convexo), siempre aparecerá este paralelogramo asociado a él.

¿Lo comprobamos? Entra en esta construcción de geogebra: https://www.geogebra.org/m/Y6DV2V6J, y modificamos el cuadrilátero moviendo los puntos azules.

Aprovechando esta propiedad, podemos recubrir el plano con el cuadrilátero que queramos. Además, los paralelogramos irán formando una malla invisible que nos guiará en la construcción.

Tan solo tenemos que ir colocando uno junto a otro, haciendo que los lados de la misma longitud coincidan. Para que los paralelogramos formen nuestra malla, tendremos que girarlos, dando media vuelta cada cuadrilátero, o lo que es lo mismo, para colocarlos, hacemos la simetría central respecto el punto medio.

{tab title=»Lo hacemos a mano» class=»green»}

El proceso es sencillo:

• Utilizaremos una revista o folleto que ya no necesitemos. En él, dibujamos un cuadrilátero cualquiera (incluso puede ser cóncavo, como en las imagen).
• Recortamos varios cuadriláteros a la vez. Así tenemos suficientes copias para hacer la composición.
• Colocamos el primero. Puedes usar el applet para ver cómo van a ir colocándolos todos.
• Los siguientes se colocan de forma que los lados iguales siempre coincidan. Cuidado: siempre van girados media vuelta unos respecto otros. Pero no voltees la figura.
• Poco a poco, podemos ir haciendo crecer la construcción.

{tab title=»Más sencillo usando la malla invisible» class=»orange»}

Podemos dibujar primero la «malla inivisible», para que nos guíe en el proceso de colocación de los cuadriláteros.
Después, podemos aprovechar para dibujar esta malla encima de ellos.

• Colocamos el primer cuadrilátero y marcamos los puntos medios de los lados.
• Con ello, dibujamos el primer paralelogramo, y a partir de él trazamos rectas paralelas para dibujar toda la malla.
• Como tenemos los paralelogramos de la malla, podemos usarlos para colocar con precisión cada nuevo cuadrilátero (los puntos medios deben coincidir con los vértices de los paralelogramos).

{/tabs}

¿Te animas a hacer tu propia construcción? Recuerda que se puede con cualquier cuadrilátero.

 

---

(*) Esta entrada participa en la Edición 1 del año 11 del Carnaval de Matemáticas,
cuya anfitriona es MoniAlus a través de su blog El mundo en un chip.

 

(*) Editado.

La entrada ha resultado ganadora del Carnaval de matemáticas. ¡Muchas gracias a todos!