Numeración griega ática
Uno de los sistemas numéricos utilizados en la antigua grecia fue el sistema ático que, con el tiempo fue sustituyéndose por otro, denominado sistema jónico. En estos sistemas, los símbolos utilizados para las cifras se tomaban de las primeras letra del nombre de esas cifras. Por eso decimos que eran sistemas acrofónicos.
Al igual que ocurre con el sistema romano, estas formas de numeración todavía conservan algunos usos incluso en la actualidad. Por ejemplo, en Grecia es frecuente utilizar el sistema ático al escribir el número del año, como podemos apreciar en esta imagen, cuya última inscripción indica, en numeración ática, el año 1828.
Imagen de Stephen Kingdom via wikimedia (CC BY-SA)
Además, los sistemas eran sumativos, de manera que el valor total del número es la suma de los valores de todas las cifras utilizadas (ver los ejemplos de la actividad «Practicamos el sistema ático»).
El sistema ático
En este sistema, se utilizaban los siguientes símbolos,
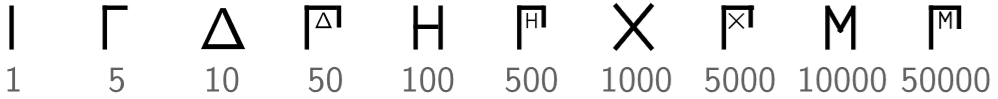
- Los símbolos del número se escriben de izquierda a derecha, comenzando por los de más valor.
- Para escribir números como el 4, al no haber símbolo específico, se repetiría varias veces el del 1: IIII.
- Para escribir números como 5 o 10, no hacemos esta acumulación, pues ya tenemos un símbolo específico.
- Números como 216, se escribirían como HHΔI, pues la suma de los valores correspondientes es 216.
- De esta forma,
- los símbolos para 1, 10, 100, 1000 y 10000 pueden escribirse hasta 4 veces seguidas.
- los símbolos para 5, 50, 500, 5000 y 50000 solo será necesario escribirlos una vez.
Como curiosidad, notar que aparece un pequeño antecedente de notación multiplicativa, al escribir los símbolos para el 50 como combinación de los de 5, Γ y de 10, Δ, resultando su producto, 50. Análogamente para 500, 5000 y 50000.
Por ejemplo, en esta estela aparecen los tributos pagados por los aliados de Atenas en la Liga de Delos, en la que se aprecian las cantidades 50, 300, 800, 33, 1000 y 1561:
Detalle de una imagen de Epigraphical Museum via Wikimedia (CC BY SA)
Practicamos el sistema ático
Con la siguiente actividad, podemos practicar la numeración ática, y ver diferentes ejemplos resueltos con los que comprender y aprender esta forma de escritura. Si no estamos seguros de cómo escribir los números, podemos comenzar viendo los ejemplos resueltos, y luego ya usar los ejercicios para comprobar que hemos aprendido a escribirlos.






