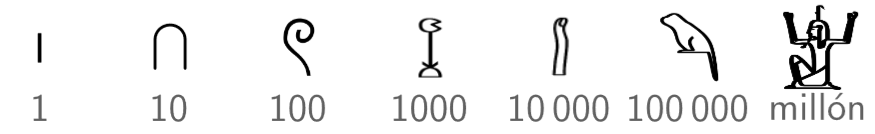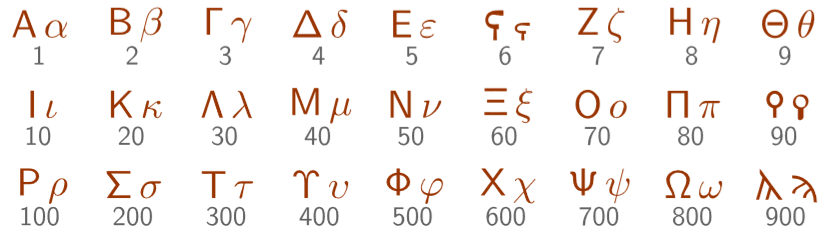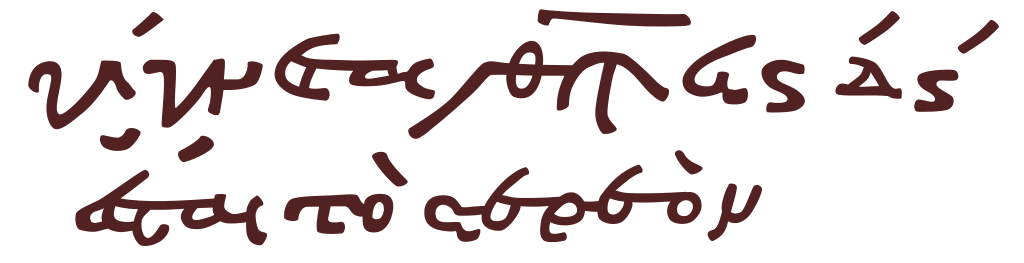Nuestras compañeras Sole y Lola, del IES Castuera, nos sugieren utilizar esta actividad para construir estrellas de Navidad utilizando matemáticas: troncos de pirámide y prismas.
Basta con crear el diseño, pulsar en «piezas» y capturar la pantalla para obtener el modelo listo para recortar.
¡Una idea genial!
Aprender a interpretar correctamente las gráficas asociadas a funciones puede resultar al principio algo confuso, especialmente cuando esas funciones representan la posición de un móvil como función del tiempo, pues se tiende a asociar la propia gráfica con el recorrido del móvil.
Por ejemplo, las gráficas siempre se generan de izquierda a derecha según avanza el tiempo; pero eso no implica que el recorrido del móvil siga esa dirección.
Para practicar este tipo de gráficas, hemos preparado unas actividades interactivas con GeoGebra, en las que podremos configurar diferentes gráficas y situaciones (altura a la que se encuentra un móvil, distancia recorrida o distancia a un punto), y visualizar diferentes posibles recorridos.
Igualmente, se incluyen algunas cuestiones para reflexionar sobre las gráficas.
En la cultura egipcia se utilizaron dos sistemas de numeración escritos: el jeroglífico, muy común en los monumentos y el hierático, utilizado más habitualmente en los papiros.
En el sistema jeroglífico, se tenían símbolos para representar la unidad, decena, centena, etc., que se repetían tantas veces como fuese necesario hasta tener el número.
Estos símbolos eran: El trazo, grillete, cuerda enrollada, flor de loto, dedo, renacuajo y el dios Heh.
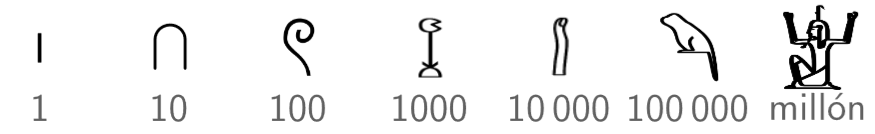
No era preciso escribirlos en ningún orden concreto, y podían colocarse de la manera en que resultasen composiciones más armoniosas; por ejemplo, colocando los símbolos en cuadrado. Incluso la orientación de las figuras podía cambiar si convenía a la lectura.
El problema de esta forma de numeración es que, para algunos números había que dibujar una gran cantidad de figuras. En el sistema hierático, había símbolos diferentes para cada unidad, decena, centena, etc., lo que permitía escribir números grandes con pocos símbolos, pero había que conocer una gran cantidad de símbolos para poder escribir números.
En la siguiente actividad podemos practicar la numeración jeroglífica egipcia, y ver diferentes ejemplos resueltos con los que comprender y aprender esta forma de escritura.
(*) Por simplificar, los ejemplos de esta actividad siempre se escribirán en línea, aunque hemos visto que esto no era necesario.
Por supuesto, para dar las respuestas de las preguntas de escritura en jeroglífico, podemos introducir los numerales en el orden que queramos.
El método clásico de escritura numérica en China comenzó a gestarse en torno al año 1500 a.C. Posteriormente, este sistema también fue adoptado en japón.
Las principales características de este sistema de numeración son:
Para construir los demás números,
En la siguiente actividad podemos practicar la numeración china y japonesa, y ver diferentes ejemplos resueltos con los que comprender y aprender esta forma de escritura.
En ocasiones, principalmente en entornos financieros, para ciertas cifras se utilizan deliberadamente otros símbolos más complicados, para evitar falsificaciones. Por ejemplo, 壱 para el símbolo de 1, como podemos apreciar en la esquina superior izquierda de este billete de 10000 yens (円), escrito como 壱万円.
Este sistema se desarrolló en la ciudad de Mileto, en el siglo V a. C. (por eso también se le conoce como sistema Milesio). Poco a poco, el sistema ático fue siendo reemplazado por el sistema jónico, de manera que en el siglo III a. C. se utilizaba de manera habitual.
En este sistema,
Future Perfect at Sunrise via Wikimedia Commons, dominio público
Reflexionamos
En ciertas ocasiones, el sistema ático todavía continúa utilizándose.
En el siguiente applet, podemos practicar la numeración ática, y ver diferentes ejemplos resueltos con los que comprender y aprender esta forma de escritura.
