¿Existe ese triángulo?

Para dibujar un triángulo, es suficiente con unir mediante segmentos tres puntos no alineados.

Sin embargo, hay ocasiones en las que conocemos algunos datos del triángulo, y queremos saber si se puede dibujar un triángulo que cumpla esas condiciones.

Por ejemplo, ¿podemos dibujar un triángulo tal que sus lados midan 5, 6 y 7cm? ¿Y que midan 4, 5 y 10cm?

También podemos preguntarnos por los ángulos: ¿habrá triángulos cuyos ángulos interiores midan 30º, 100º y 50º? ¿y que midan 30º, 60º y 50º?

Cuestiones relacionadas con la docencia

{tab title=»¿Cómo resolverlo?» class=»blue»}

Una forma de resolver este problema es mediante las técnicas para dibujar triángulos a partir de sus elementos:

Si es posible dibujarlo, entonces el triángulo existe. Si no es posible, entonces es que no existe.

Es importante conocer y saber llevar a cabo estas técnicas, porque permiten que el alumno interiorice sus conocimientos matemáticos a través de su manipulación (circunferencias, distancias, ángulos y su medida -con el transportador o con el compás-).

Por otra parte, este tipo de problemas también nos ofrecen una gran oportunidad para que el alumnado constate una de las grandes utilidades de las matemáticas:

Podemos demostrar o decidir si una afirmación es cierta utilizando únicamente nuestros razonamientos y nuestros conocimientos matemáticos.

El alumnado comprobará cómo el conociminento matemático le permite ahorrar tiempo y esfuerzo (la construcción del triángulo), y además tenemos mayor certeza de nuestros resultados, pues estamos libres de pequeñas imprecisiones que puedan cometerse en el proceso de dibujo.

En este caso, aprenderemos a decidir si existe el triángulo de dos maneras:

• Si conocemos la medida de los tres lados, comprobaremos la propiedad triangular.
• Si conocemos la medida de los tres ángulos, comprobaremos que juntos suman un ángulo llano.

Además, estas importantes propiedades del triángulo también son, a su vez, muy sencillas de demostrar visualmente, con lo que esas demostraciones nos pueden servir para introducir al alumnado en el razonamiento matemático.

{tab title=»¿Cómo interesar al alumnado?» class=»green»}

Es posible que, resolver actividades en las que simplemente se pida que aplicar la propiedad triangular o la suma de los ángulos de un triángulo pueda resultar poco atractivo, con lo que los alumnos las realicen con poco interés y el aprendizaje resulte poco significativo.

Por ello, se ha preparado una actividad que:

• Incluiya las explicaciones teóricas de manera visualmente atractiva.
• Permita interactuar con estas explicaciones. Así propiciamos que el alumnado tome el protagonismo del proceso de enseñanza-aprendizaje y asimile mejor los conocimientos.
• Contenga una parte práctica que permita afianzar y comprobar los conocimientos adquiridos.

Nuevamente, nos enfrentamos al problema de que la parte práctica pueda resultar poco atractiva. En este caso, y para evitar esto, se ha optado por:

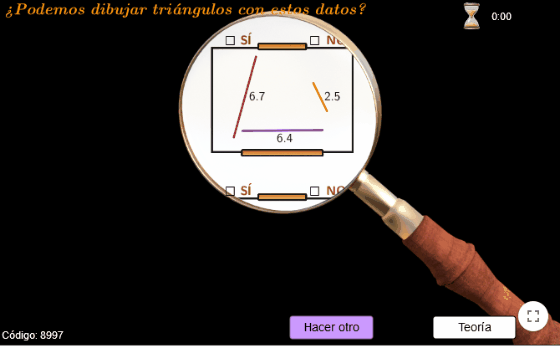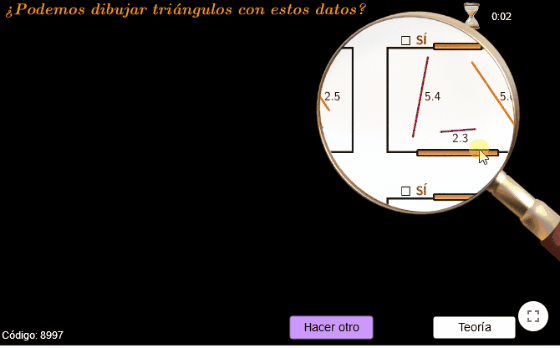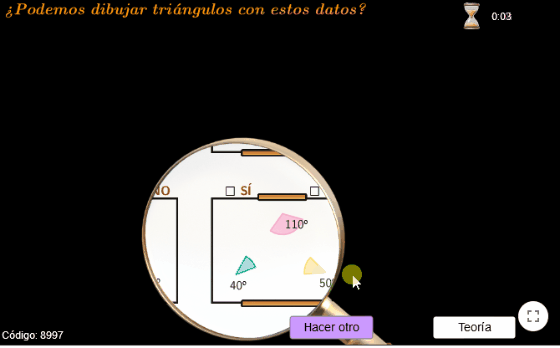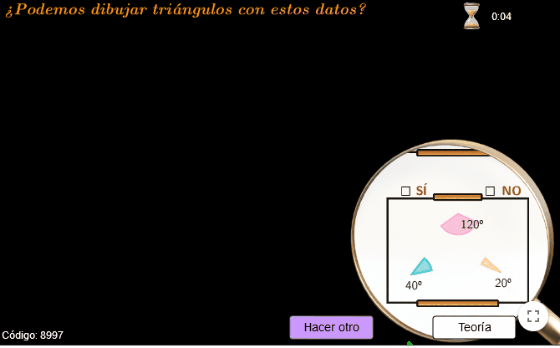
• realizar las preguntas en un entorno visualmente atractivo: en lugar de plantearlas mediante un texto estático con las medidas de esos elementos, se utiliza una representación dinámica, donde están dibujados en el «lienzo de un artista», y constan de algo de movimiento que hará que focalicemos la atención en los datos y la pregunta.
• introducir elementos de gamificación:
  • utilizamos una lupa que, al desplazarla por la pantalla, nos mostrará un ejercicio u otro y nos permitirá responderlos.
  • un cronómetro medirá el tiempo que tardamos en responder y el tiempo total. Completar el «juego» en el menor tiempo posible motivará a los alumnos a practicar hasta tener los conocimientos completamente interiorizados.
  • se pueden realizar tantas fichas como se quiera y, aunque se penalizan las respuestas incorrectas, se conserva la puntuación más alta alcanzada.

{tab title=»¿Visualizamos la teoría?» class=»orange»}

La actividad propuesta está dividida una parte teórica, con tres apartados con la información sobre cómo dibujar los triángulos:

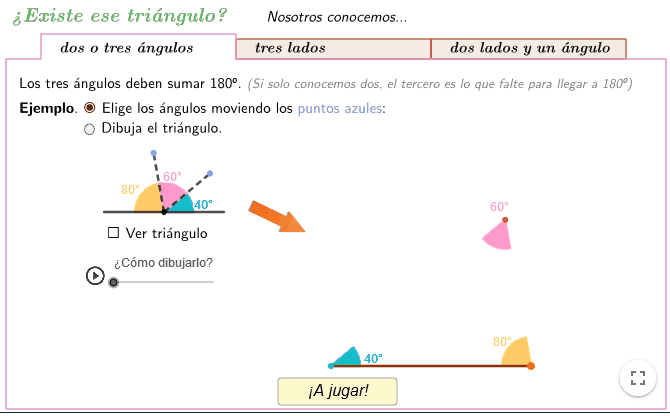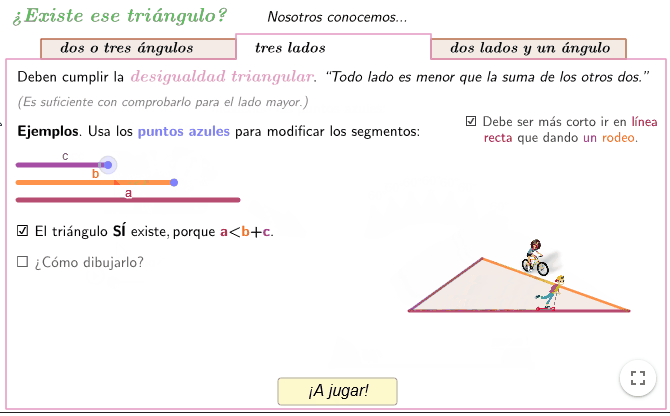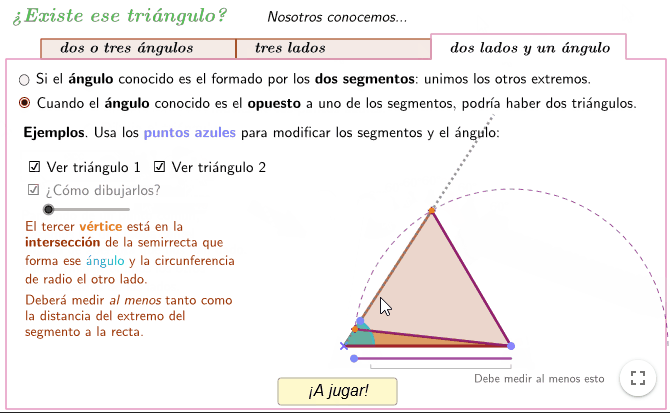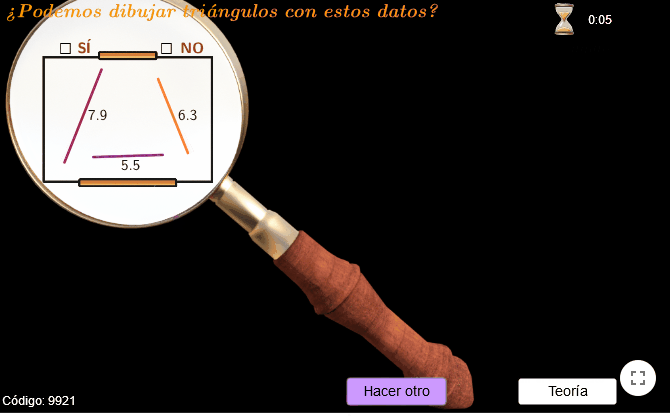
• Conocidos los tres ángulos. Podemos visualizar de manera interactiva (eligiendo nuestros propios ángulos) y explicaciones paso a paso cómo realizar el dibujo y también podemos ver una demostración visual de que la suma de los ángulos es un ángulo llano.
• Conocidos los tres lados. Tenemos una demostración visual de la propiedad triangular, junto a las explicaciones del proceso para dibujar el triángulo a partir de los lados que elijamos, y cómo decidir si el triángulo existe.
• Conocidos dos lados y un ángulo. A modo de ampliación, se verá cómo resolver este caso, con las dos posibilidades que se nos presentan: el ángulo es el formado por los dos lados, o bien que el ángulo sea el opuesto a uno de ellos. Puede ser interesante que los alumnos visualicen cómo, según los datos, un problema puede no tener solución o bien tener una o incluso dos soluciones.

{/tabs}

 Nuestra actividad

Juntando las ideas anteriores, se ha elaborado la siguiente actividad con la que nuestro alumnado pueda aprender a razonar matemáticamente si existe un triángulo que cumpla ciertas condiciones, y pueda practicarlo de forma lúdica.
(Hacer clic en la imagen para cargar la actividad, o bien en este enlace para verla en GeoGebra.)

Instrucciones:

Modo Juego:

• Mueve la lupa para visualizar cada uno de los 6 posibles triángulos que queremos formar y marca la casilla según creas que puede o no existir.
• En cada ficha, habrá tres preguntas de «conocidos los tres lados» y tres de «conocidos los tres ángulos».
• Cuando hayamos respondido a los 6 triángulos, podremos pulsar el botón para Corregir.
• Si todas las respuestas son correctas, obtendremos 2,5 puntos. Conun fallo, tendremos 1 punto. Con dos fallos, 0 puntos. Con 3 o más fallos, iremos perdiendo puntuación.
• Pulsando el botón Hacer Otro, nos propondrán otra ficha.
• Podemos intentar tantas fichas como queramos. Se conservará la calificación más alta y se lleva la cuenta del número de intentos.

Teoría: Aprenderemos a distinguir cuándo existe el triángulo y los pasos que debemos seguir para dibujarlo. Veremos tres posibilidades, según conozcamos:

• Dos (o tres) ángulos.
• Los tres lados.
• Dos lados y un ángulo.

 

Este post forma parte del Carnaval de Matemáticas, que en esta octogésima novena edición,
también llamadada 11.3, está organizado por Fran Martínez Seoane a
través de su blog Astronautas y Robots vs Coronavirus.