Las matemáticas detrás del concurso Atrapa un millón
¿Qué probabilidad tendrías de ganar algo sin tener ni idea en ninguna de las preguntas? En el sentido de teoría de la decisión con incertidumbre y en caso de dudar en una pregunta, ¿es mejor apostar todo a una respuesta o repartir los fajos de billetes?
Para resolver todas estas cuestiones que seguro te quitan el sueño en Ciencia explicada han creado un simulador online y te explican el desarrollo matemático en el que está basado.
Funciones con Jclic
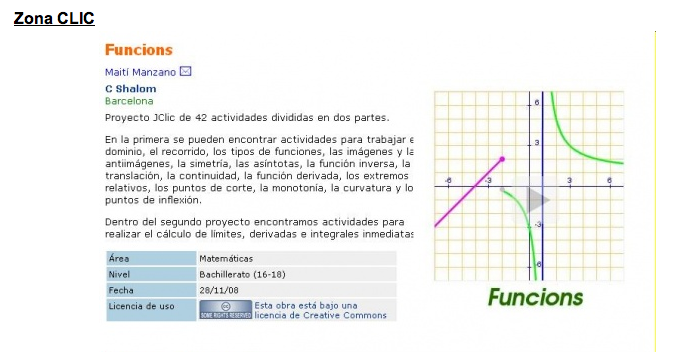
42 actividades divididas en dos partes.
En la primera se pueden encontrar actividades para trabajar el dominio, el recorrido, los tipos de funciones, las imágenes y las antiimágenes, la simetría, las asíntotas, la función inversa, la translación, la continuidad, la función derivada, los extremos relativos, los puntos de corte, la monotonía, la curvatura y los puntos de inflexión.
Dentro del segundo proyecto encontramos actividades para realizar el cálculo de límites, derivadas e integrales inmediatas.
Nos proporciona un código para poder incrustar la actividad en un sitio web, moodle, o blog.
Funciones con Jclic
42 actividades divididas en dos partes.
En la primera se pueden encontrar actividades para trabajar el dominio, el recorrido, los tipos de funciones, las imágenes y las antiimágenes, la simetría, las asíntotas, la función inversa, la translación, la continuidad, la función derivada, los extremos relativos, los puntos de corte, la monotonía, la curvatura y los puntos de inflexión.
Dentro del segundo proyecto encontramos actividades para realizar el cálculo de límites, derivadas e integrales inmediatas.
Nos proporciona un código para poder incrustar la actividad en un sitio web, moodle, o blog.
Límites y continuidad
| Introducción intuitiva al concepto de límite |  |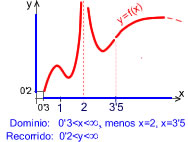
 Propiedades básicas sobre límites |
|
| Métodos para el cálculo de límite( Descargar ) |
|
 |
|
Unidad didáctica del Proyecto Descartes con numerosas escenas interactivas para introducir al alumnado, mediante la manipulación de las mismas, en el concepto de continuidad de una función, así como en la catalogación de los casos en los que la función no es continua. La unidad está también disponible en Inglés |
|
Se analizan las propiedades fundamentales y se obtienen las propiedades operativas de los límites se obtienen lson la base de los métodos de cálculo de límites. Por último se dedica un apartado al análisis de los llamados límites indeterminados, mostrando con ejemplos el significado de estas indeterminaciones y aclarando un concepto que produce muchas confusiones en los alumnos. |
|
Unidad didáctica del Proyecto Descartes que analiza detenidamente las hipótesis y la tesis de los teoremas de Bolzano y de Weierstrass sobre funciones continuas y estudia alguna de sus aplicaciones más importantes. |
Fuentes. Página de Paco Gonzálesz , Wikididáctica del INTEF y Planeta Matémático