Entretenimiento y Arte con Posiciones Relativas y polígonos

Utilidad de las posiciones relativas

• ¿Por qué es importante conocer la posición que puede tener una figura con respecto otra?
• ¿Por qué es importante ponerles nombre?
• Con este pequeño juego podremos aprender los diferentes tipos de posiciones relativas (clic en la imagen para activarlo), y con las actividades de «entretenimiento» veremos algunos motivos por los que resulta importante conocerlos.

---

Uno de los motivos de la importancia de aprender las posiciones relativas es que, al conocer las distintas posibilidades que hay, abrimos la puerta a saber cómo realizar nuestras creaciones artísticas y qué efectos podemos darle. Por ejemplo:

• La idea de tangencia: cuando dos figuras son tangentes en un punto, ocurre que «muy cerca» de ese punto las figuras son prácticamente iguales.
  Podemos aprovechar las tangencias para pasar de una figura a otra sin que se noten cambios bruscos.
• Por el contrario, cuando dos figuras son secantes, pasan por el mismo punto pero, cerca suya, no se parecen nada una a la otra. Podemos aprovechar esto para dibujar varios caminos que van en direcciones distintas y, simplemente se cruzan en ese punto.
• El hecho de restringir un punto a que pertenezca a una circunferencia puede parecer poco importante, pero nos llevará a utilizar giros en nuestras figuras,
• Igualmente, tener un punto sobre una recta y deslizarlo sobre ella nos llevará a los conceptos de traslación y homotecia, que utilizaremos para cambiar la escala de nuestros dibujos o colocar objetos en distintos lugares.

En las actividades de entretenimiento y arte podremos indentificar estos elementos.

Entretenimiento con un poco de arte

{tab title=»Arte con circunferencias» class=»red»}

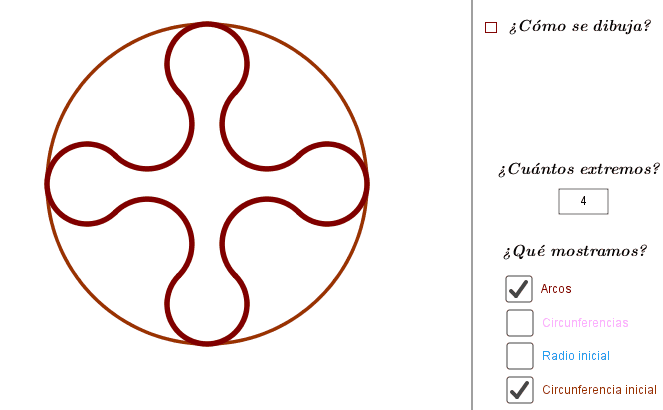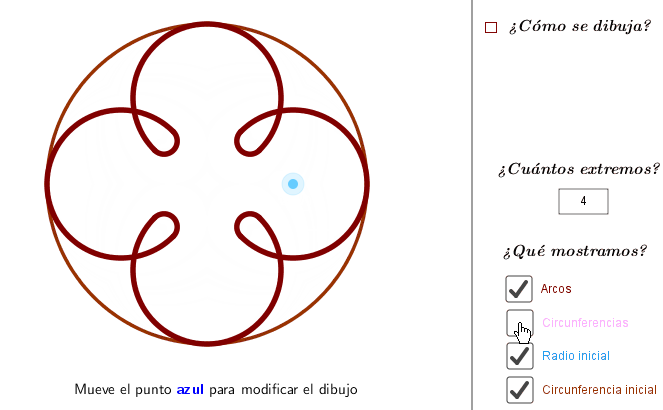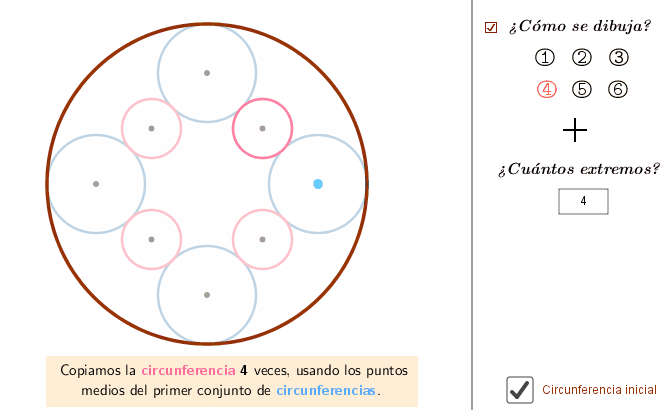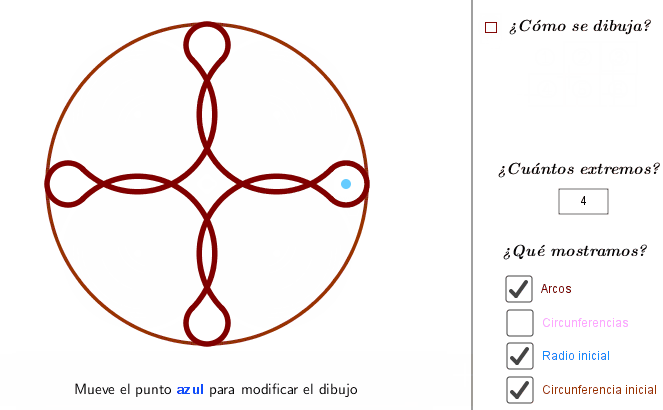
• Utilizaremos el concepto de circunferencias tangentes y secantes para una primera creación artística. Podemos utilizar el applet para ver diferentes posibiliades o generar una plantilla con la que después hacer nuestra propia creación a mano.

Fíjate en que para dibujar las circunferencias tangentes, utilizamos la propiedad de que los centros y el punto de tangencia están alineados.

¿Aprecias la direfencia en el efecto que causa cuando los arcos de circunferencia son tangentes o son secantes?

 

 

{tab title=»Arte gótico» class=»grey»}

• Utilizando la misma idea que con la construcción anterior, a partir de un polígono regular podemos recrear bonitas figuras que nos recuerdan al arte gótico. Para hacer más artística nuestra composición, podemos darle un efecto 3D al contorno de las líneas.
• Pulsa en la animación para cargar la actividad e interactuar con ella. En el propio applet encontrarás las indicaciones sobre cómo hacer la composición paso a paso.

---

La parte más difícil para hacer esta construcción a mano es trazar una circunferencia tangente a otras dos cuando conocemos el punto de tangencia.

---

Para hacer tu propia creación puedes imprimir el applet como plantilla, dejando visibles los elementos que necesitas si alguno de los pasos te resulta demasiado complicado.

{tab title=»Curvas y rectas» class=»blue»}

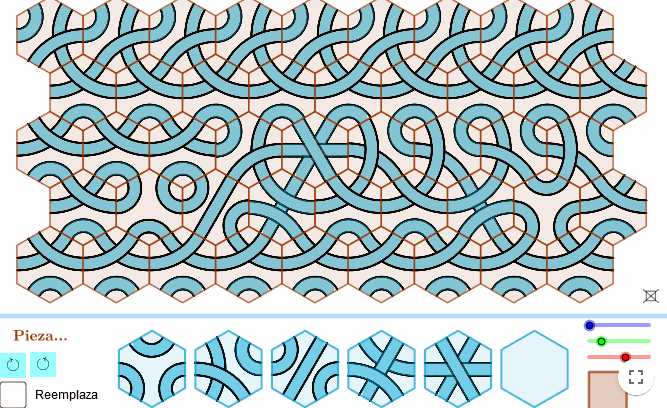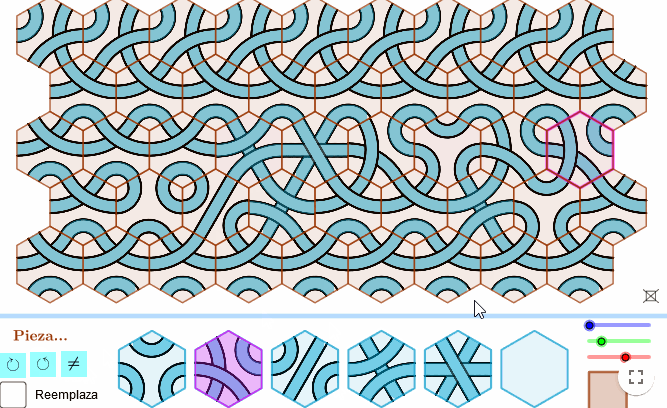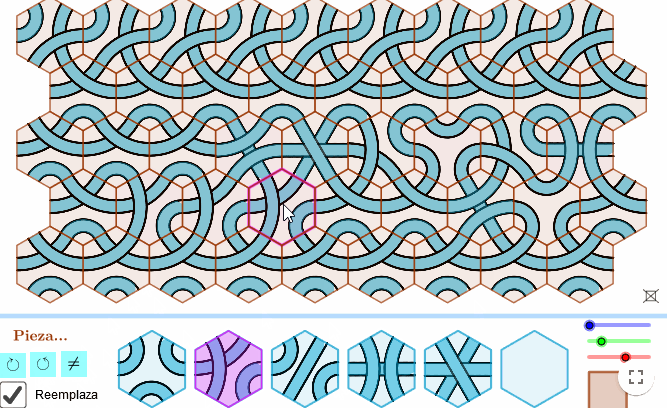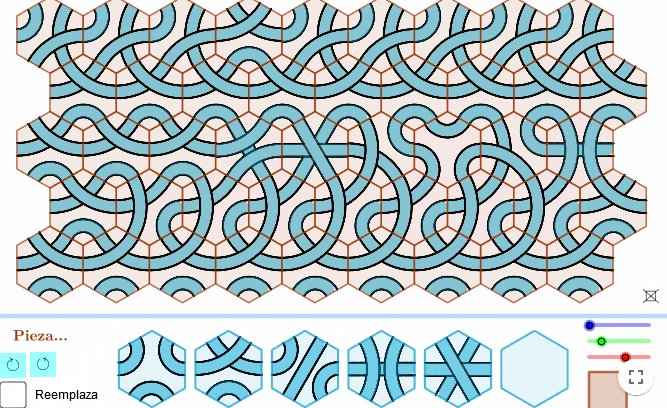
Igualmente, podemos crear un pequeño juego para crear dibujos artísticos a partir de sencillas fichas que enganchan una con otras.

• Para diseñar las fichas, aprovechamos que los hexágonos rellenan el plano sin dejar huecos «teselan».
• Haciendo que nuestros dibujos siempre acaben en el medio de los lados de los hexágonos, conseguiremos que ajusten bien entre ellos.
• Tan solo tendremos que crear unos cuantos patrones para que, al combinarlos, podamos hacer todo tipo de creaciones artísticas. 

---

---

Piezas

---

Más información

{tab title=»Plegados de Miura» class=»green»}

• Los plegados de Miura permiten doblar un folio con un solo movimiento. Por ejemplo, haciendo estas dobleces en un mapa, podríamos plegarlo completamente de una sola vez con tan solo ir juntando los extremos.
• Esta propiedad es útil para el plegado de paneles solares, tanto en la Tierra como en el espacio, al permitir el uso de un solo motor (movimiento en una única dirección) en lugar de dos.
• Puede hacerse a partir de cualquier teselación con paralelogramos que no sean rectángulos.

Pero fíjate: para describir el diseño de esta actividad, necesitamos utilizar nuestro vocabulario ralacionado con las posiciones relativas. Para hablar de los giros y ángulos, de cómo redimensionar y construir los los paralelogramos, etc. ¿Qué herramientas matemáticas necesitarías para describir lo que ocurre?

---

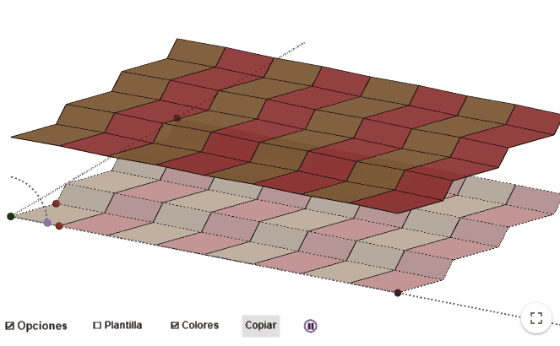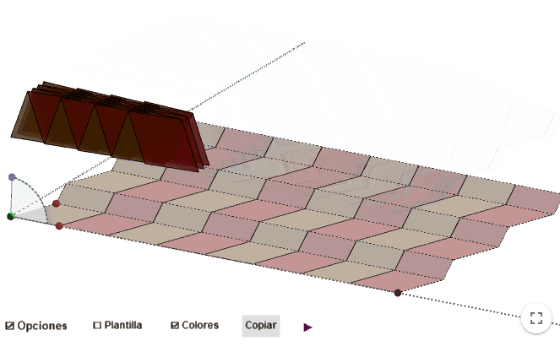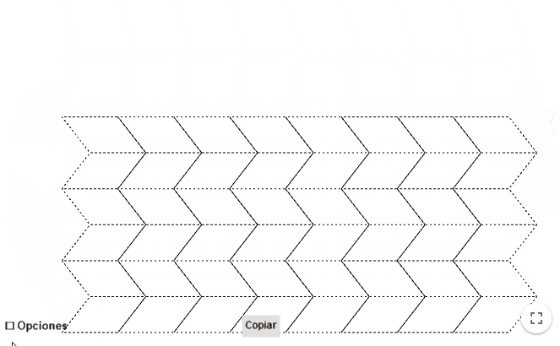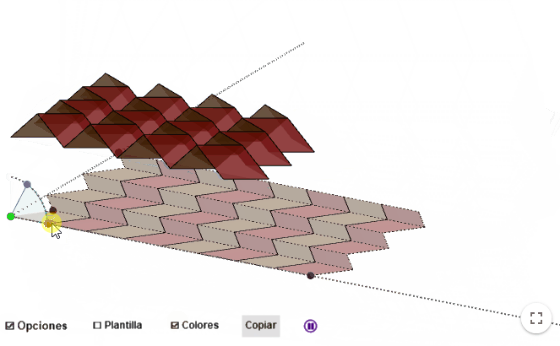
¿Lo hacemos a mano?

---

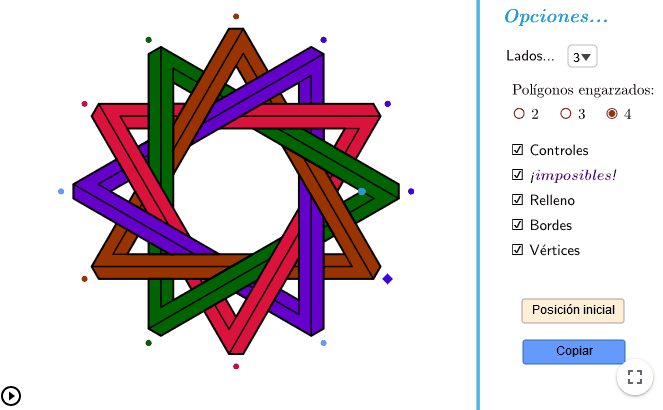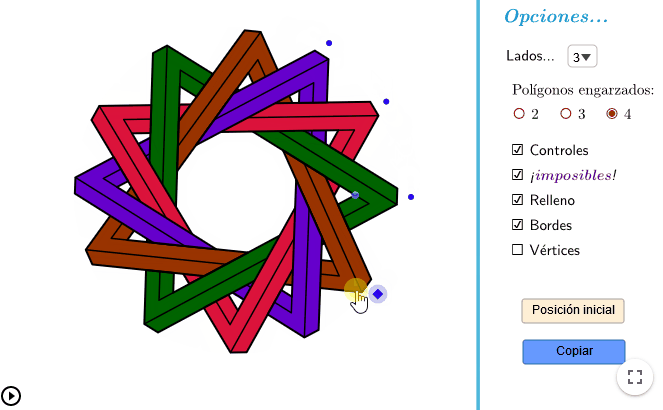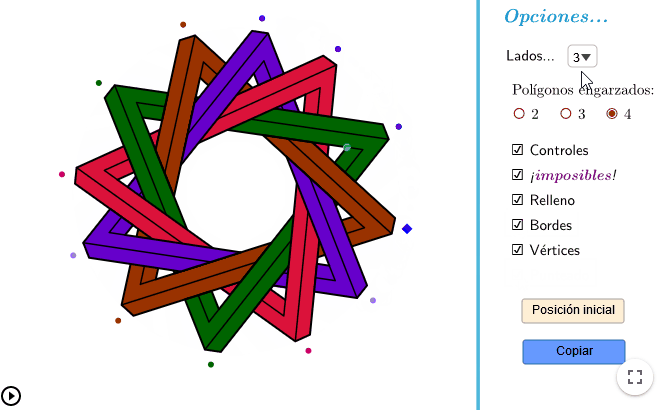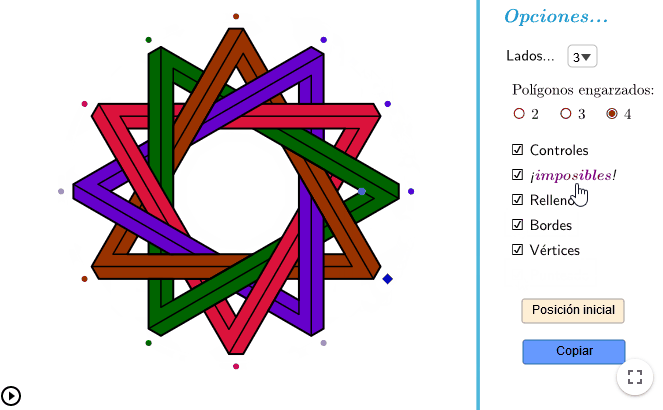
Plantillas de ejemplo

---

• Al igual que en otras actvidades, si pensamos en cómo describir la construcción, necesitamos nuestro vocabulario de posiciones relativas. Por ejemplo: para poder dibujar los polígonos engarzados, no pueden tener cualquier grosor.
• Para poder describirlo con precisión, piensa cómo está relacionado con punto interior/exterior a una circunferencia, circunferencias concéntricas, tangentes, etc.

{/tabs}

[Editado]

El post resultó ganador de la edición de junio del Carnaval de Matemáticas.