¿Por qué son notables esos puntos del triángulo?
Un triángulo podría parecernos poca cosa. Después de todo, consiste únicamente en tres puntos no alineados. Sin embargo, los utilizamos en todas partes: arte, arquitectura, navegación, señales de tráfico, crear mapas, imágenes 3D para videojuegos…
Son tan importantes que se han estudiado miles de propiedades y elementos notables de ellos. Incluso hay una enciclopedia de Centros del triángulo que recoge ¡más de 38000 puntos asociados a ellos!
Vamos a analizar algunas situaciones/juegos con las que veremos la utilidad de los 4 puntos y rectas más importantes «notables» asociados al triángulo.
{tab title=»Buscando el equilibrio» class=»blue»}
Para cualquier triángulo, existe un punto que es su punto de equilibrio:
- Si lo ponemos plano, apoyado sobre ese punto, el triángulo se mantiene en equilibrio sin caerse hacia ningún lado.
- Si lo sujetamos en vertical, agarrando por ese punto, no importa en qué posición esté, que no se girará.
¿Cómo encontrar ese punto mágico?
Vamos a investigarlo con esta actividad (haz clic en la imagen para cargar la actividad e interactuar con ella):
Instrucciones
- Podemos modificar el triángulo desplazando sus vértices.
- El gancho tirará del punto azul. Si lo elegimos bien, el triángulo no girará mientras lo está moviendo.
- Para elegir el punto del que tiraremos con el gancho, primero situamos el punto naranja, y luego el azul.
- Haciendo clic en el gancho, haremos que recoja el triángulo. Volviendo a hacer clic, lo devolverá a su posición inicial.
Reflexiona
- Este punto «mágico» se denomina baricentro, porque es el centro de gravedad del triángulo (los prefijos bar y bari significan peso).
- ¿En qué punto de cada lado debemos situar el punto naranja para encontrar el baricentro? Las líneas que los unen con los vértices se denominan medianas.
- Al activar las «pistas» para el punto azul, la mediana se divide en tres partes iguales. ¿Qué relación guardan con el baricentro?
- ¿Dónde debemos situar el gancho para que al sujetar en cualquier punto de una de las medianas, el triángulo no gire al arrastrarlo?
Nuestro turno
Buscaremos el centro de gravedad -baricentro- para poder apoyar un triángulo sobre algo fino, como un bolígrafo o nuestro dedo, sin que se caiga. Para ello:
- Recortamos un triángulo que nos guste en una superficie rígida -por ejemplo cartón-.
- Dibujamos un par de medianas -recta que une un vértice con el punto medio del lado opuesto-.
- Ya sabemos que su intersección es el baricentro. Si queremos, podemos comprobar que, efectivamente, la tercera mediana pasa por ahí.
- Con cuidado, lo colocamos apoyando el baricentro sobre la punta de un bolígrafo, nuestro dedo… ¡Se mantiene en equilibrio!
También podemos comprobar que ocurre como en la actividad: al arrastrar desde el baricentro, el triángulo no se gira.
Aquí tenemos un ejemplo de cómo podría ser nuestro experimento, recortando un triángulo de cartón:
{tab title=»¿Quién está más cerca?» class=»green»}
Tenemos varios amigos repartidos por la ciudad. ¿Sabríamos decir qué cosas están más cerca de cada uno?
- Asignando a cada amigo un color con el que colorear todo aquello que está «más cerca suya», obtenemos una bonita composición artística.
- Pero… ¿cómo hacemos para dividir el mapa?
- Vamos a jugar con esta actividad para investigar cómo se hace. Pulsa en la imagen para cargar la actividad e interactuar con ella:
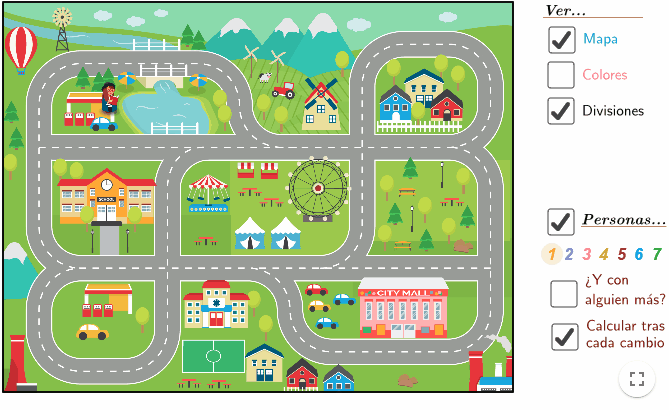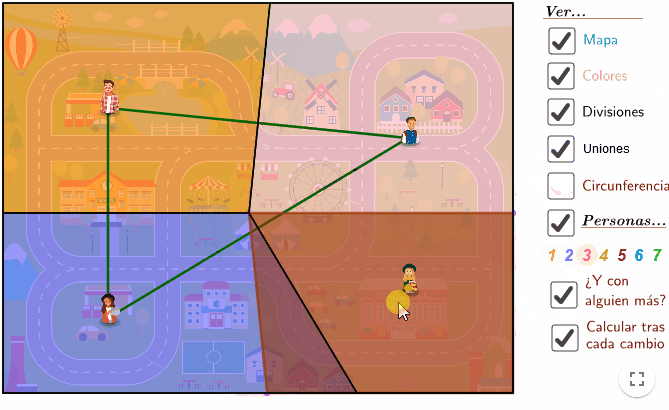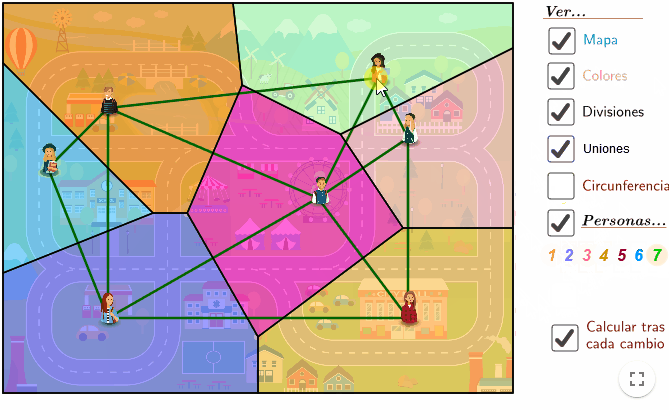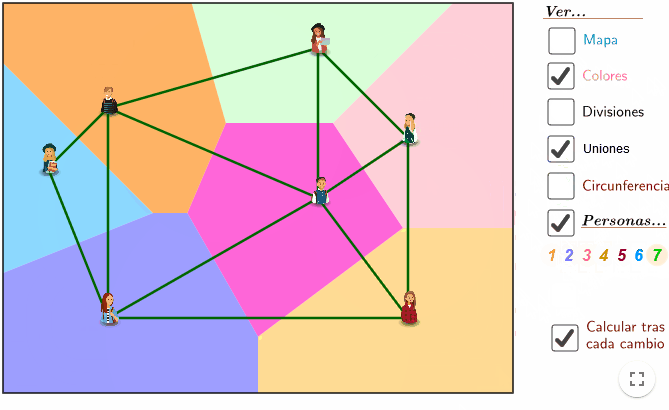
Instrucciones
- ¿Qué línea tenemos que trazar para dividir el mapa?
- Será justo la de los puntos que están a la misma distancia de las dos personas, ¿pero cuál es?
- Pues la que pasa por «el medio de los dos»… que precisamente se llama mediatriz.
- Uniendo las dos personas, podemos encontrar una pista de cómo trazarla: fíjate, la mediatriz es perpendicular a la línea que une a las personas.
– Si pasamos a tres personas (pulsamos en el número «3» en la zona de la derecha)
- Bastará con trazar las nuevas mediatrices y «recortar» la parte que sobre de las dos zonas anteriores.
- Para hacernos mejor una idea, podemos marcar la casilla «¿Y con alguien más?» y ver qué ocurre al cambiar de sitio a la tercera persona.
- Interesante: con tres personas, hay un punto en común a las mediatrices. Ese punto está a la misma distancia de las tres personas. Se llama circuncentro, porque con centro en él podemos trazar una circunferencia circunscrita (que pase por las tres personas), tomando como radio la distancia a las tres, que es siempre la misma).
- ¿Qué tipo de triángulo deben formar para que el caiga en uno de los lados?¿Y para que esté dentro del triángulo?¿Y fuera?
¿Y con más personas?
- Podemos ir siguiendo un proceso similar a cuando pasamos de dos a tres personas.
- La diferencia y es que normalmente ya no hay un único punto en común sino varios puntos, comunes a grupos de personas.
- Investiga qué ocurre con las circunferencias marcando la casilla Circunferencia y cambiando el centro de posición.
Desmarca la casilla Mapa para ver únicamente la composición de colores. ¿Qué te parece esta obra de arte? Habremos creado un Diagrama de Voronoi, que es una forma matemática de dividir planos en zonas, que tiene gran cantidad de aplicaciones prácticas. En este vídeo tienes una pequeña explicación, y en este enlace, cómo aplicarlo… ¡a la colocación en el fútbol!
¿Qué se obtiene al unir las personas?
- Si nos fijamos, al unir las personas de las zonas que están conectadas, se va obteniendo una bonita «triangulación» (dividimos el mapa en triángulos).
- Se llama triangulación de Delaunay, y también tiene muchas aplicaciones prácticas, como el modelado de figuras a ordenador.
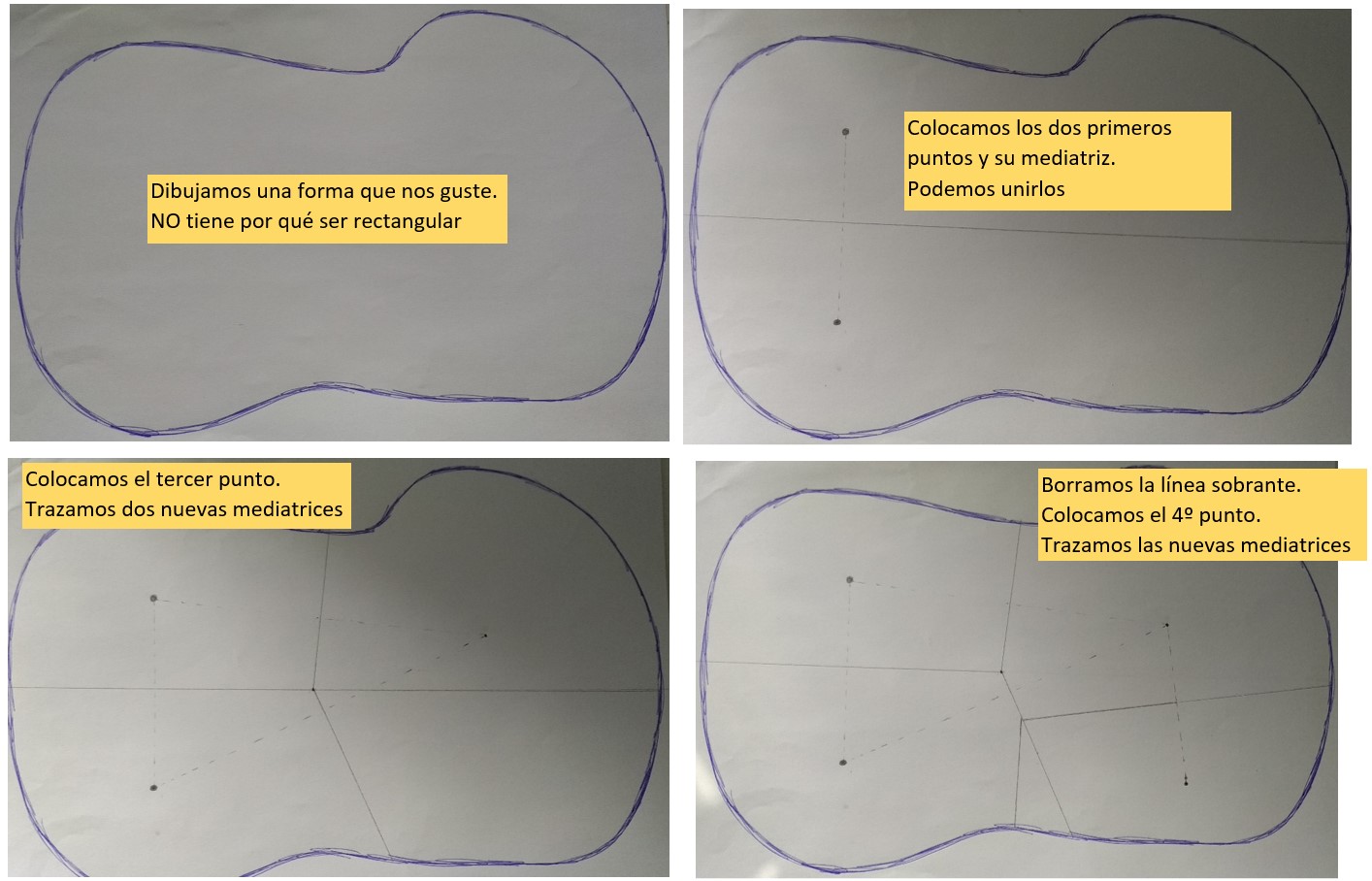
Nuestro turno
- Elegimos un mapa (de una ciudad, campo de fútbol, parque,…), y el número de personas que queremos usar para dividirlo. En vez de personas, pueden ser bares, parques… Por ejemplo, ¿cómo queda dividida en zonas mi ciudad con los parques infantiles que tiene?
- Podemos obtener el mapa de una captura de pantalla de Google Maps, dibujarlo a mano, o incluso inventarlo. Si solo queremos la composición artística, podemos usar un folio en blanco.
- Trazamos, poco a poco el diagrama (cada vez incluyendo un punto más). Como hay que ir borrando zonas, lo haremos a lápiz y sin marcar mucho.
- Recuerda: las mediatrices pasan por el punto medio y son perpendiculares a la recta que une a las personas. Puedes usar la anterior actividad de GeoGebra para asegurarte de estar haciéndolo correctamente.
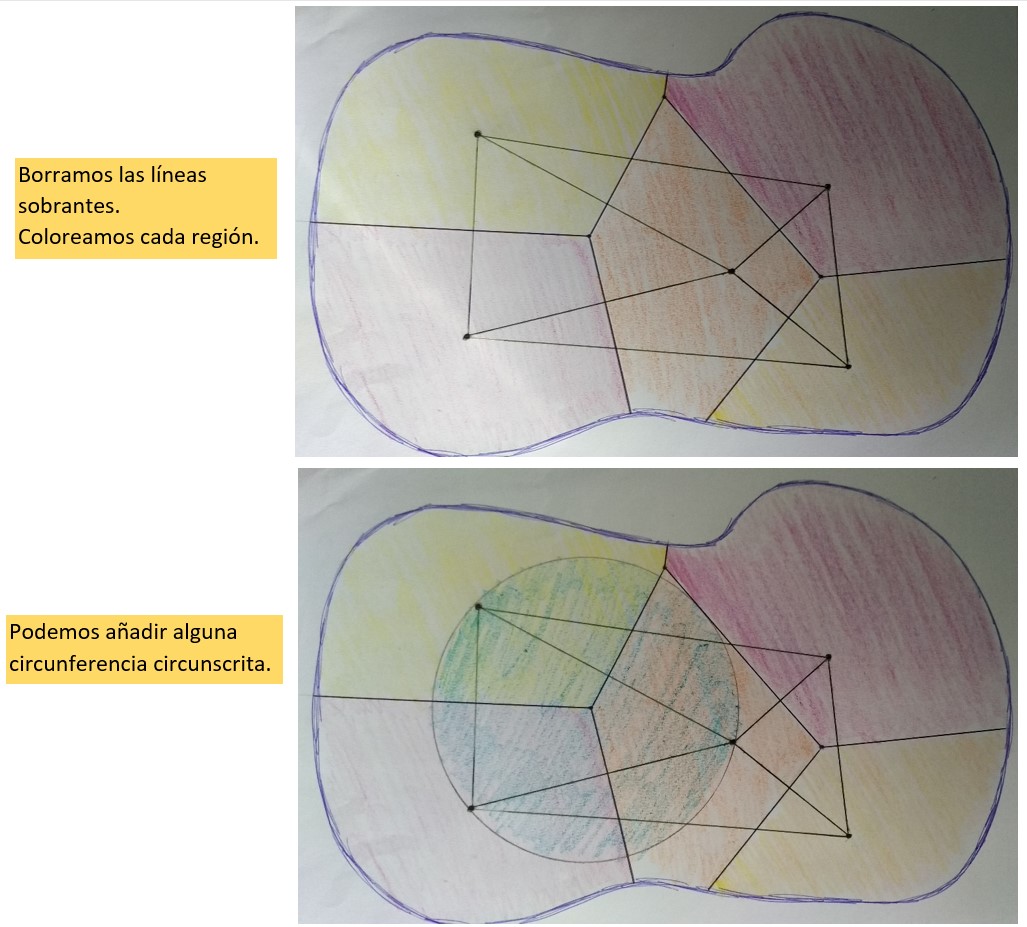
- Por último, coloreamos cada una de las zonas que hemos obtenido.
- Si queremos, podemos incluir la triangulación de Delaunay o alguna circunferencia circunscrita en el dibujo.
Aquí tenemos un ejemplo de cómo hacer nuestra composición artística:
Para saber más
- Fíjate que trazando mediatrices hemos encontrado una forma muy artística de dividir una figura en diferentes trozos.
- Este procedimiento puede ampliarse a tres dimensiones, para descomponer objetos mediante la «fractura de Voronoi».
Aquí tenemos un ejemplo donde se utiliza:

{tab title=»¿Hacia dónde lanzamos el balón?» class=»orange»}
Unos niños están jugando al balón en el patio de su urbanización.
- ¿Hacia dónde deben lanzarlo para que, al rebotar, vuelva hacia ellos?
- ¿Sabríamos describirlo matemáticamente?
- Cuando lo consigas para los tres, fíjate que hay un punto por el que siempre pasarán los balones. Pulsa en «Razonar» para averiguar su nombre.
- Reto: coloca los tres balones en ese punto (puedes moverlos arrastrando con el ratón).
Para encontrar la solución, los balones tienen que recorrer unas rectas que se llaman alturas, ¿por qué se llamarán así? Haz clic en la imagen para cargar la actividad y poder interactuar con ella, y pulsa en Se llaman alturas para averiguarlo.
Instrucciones
- Pulsa en los niños para que lancen el balón o se detenga.
- Siempre lanzamos hacia los puntos rojos. Pulsa en ellos para ver el recorrido que hará el balón.
- Activando la casilla Rebotes, veremos hacia dónde se dirigirá el balón tras rebotar en la pared. ¡Podemos lanzarlo por encima de los edificios!
- Activando la casilla Razonar, tendremos indicaciones de hacia dónde apuntar para que el balón vuelva a nosotros.
▶ Se llaman alturas
- Pulsa en los niños para que lancen el balón o se detenga.
- Activando la casilla Razonar se nos explica por qué las alturas de un triángulo reciben ese nombre.
- Las alturas tienen un punto en común, que se denomia ortocentro, porque es el punto por donde pasan esas rectas ortogonales -perpendiculares-.
¿No te parece curioso?
Estamos viendo que las rectas «notables» tienen un punto en común.
- En ocasiones, como con el baricentro o el circuncentro, puede razonarse que tiene que existir.
¿Cómo lo razonarías? - En otras, los matemáticos tienen que hacer una demostración.
- Esta capacidad de la matemática para demostrar cosas que no parecen evidentes ha fascinado desde siempre a muchos científicos.
De hecho, Albert Einstein dijo una vez:
«Había afirmaciones como, por ejemplo,
la referente a la intersección de tres alturas de un triángulo en un solo punto que,
a pesar de no ser en absoluto evidentes,
podían, sin embargo, demostrarse con tal grado de certidumbre que
cualquier duda parecía fuera de lugar.
Esa lucidez y esa seguridad me produjeron una impresión indescriptible.»
- ¿Y tú qué opinas sobre las matemáticas?
{tab title=»Colocando una jardinera» class=»red»}
En la zona común de una urbanización, quieren instalar varios paseos con jardineras a los lados.
- Los paseos comenzarán en los extremos de los edificios y -para contentar a todos los vecinos- quieren que se mantengan siempre «a la misma distancia» de los edificios.
- Además, han pensado en instalar una fuente, que también quieren que esté a la misma distancia de los tres edificios.
¿Les ayudamos a trazar esos paseos? Haz clic en la imagen para cargar la actividad e interactuar con ella.
Instrucciones
- Pulsa en los botones para ver la fuente o una persona en el paseo.
- Podemos modificar la posición de ambos arrastrando con el ratón.
- La «sombra» nos ayudará a medir las distancias a los edificios.
- Moviendo los puntos verdes, podemos modificar la dirección en la que se irá trazando el paseo.
- Pulsando en los edificios o en sus bordes, podemos mostrarlos y ocultarlos.
- Marcando Razonar, podemos ver pistas para la resolución del problema.
Reflexionamos
- Un primer intento podría ser trazar los paseos para que fuesen al punto medio del lado contrario. Verás marcados esos puntos medios.
- Sin embargo, normalmente eso no soluciona el problema. Compruébalo moviendo los extremos del triángulo. Investiga cómo tienen que ser los edificios para que el punto medio sí nos valga.
- ¿Crees que siempre será posible encontrar un lugar donde colocar la fuente? Activa la casilla Razonar para encontrar la solución.
- Verás que ese punto se denomina incentro, porque es el centro de la circunferencia inscrita en el triángulo, es decir, una circunferencia que está dentro del triángulo y toca a cada lado en un solo punto -es tangente a los lados-.
- Las rectas que hemos trazado se denominan bisectrices, porque dividen -bisecan- el ángulo en dos partes iguales.
{/tabs}
Estos son nuestros elementos notables
En total, hemos visto los 4 tipos de rectas y puntos más importantes asociados a un triángulo… de los muchos que hay.
- Medianas y baricentro, en Buscando el equilibrio.
- Mediatrices y circuncentro, en ¿Quién está más cerca?
- Alturas y ortocentro, en ¿Hacia dónde lanzamos el balón?
- Bisectrices e incentro, en Colocando una jardinera.
También son interesantes el Punto de Fermat (en esta actividad puedes ver alguna de sus utilidades), o la recta de Euler (que podemos aprender como «ampliación» en la actividad siguiente).
Por último, tenemos un juego interactivo (haz clic en la imagen para cargar la actividad e interactuar con ella), con un pequeño resumen de lo que hemos aprendido: rectas, puntos ¡circunferencias! y propiedades asociados a un triángulo.
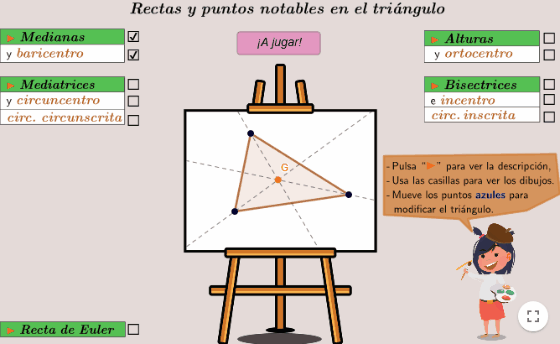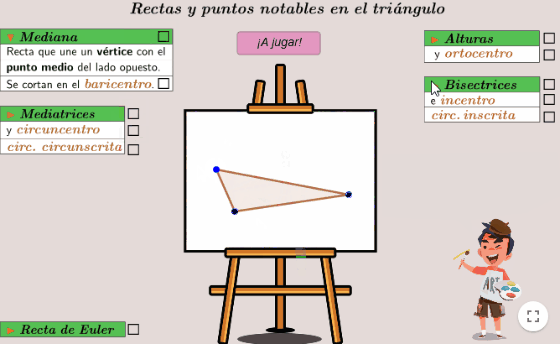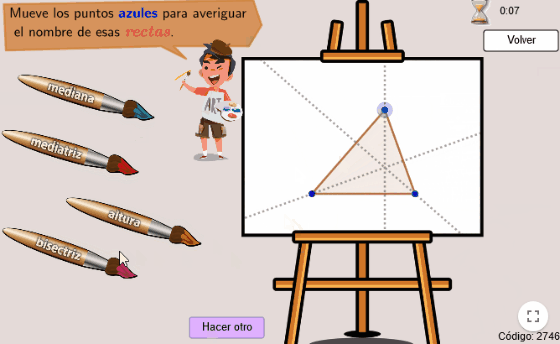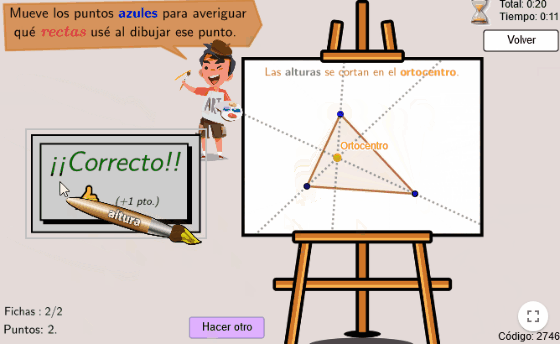
Instrucciones
- Conociendo las rectas y puntos notables y observando cómo cambia el dibujo al mover los puntos azules, podremos averiguar la respuesta.
- Para responder, pulsamos sobre el pincel correspondiente.
- Podemos arrastrar los pinceles para cambiarlos de posición.
- Cada pregunta correcta vale 1 punto, pero cada fallo nos penalizará 1 punto.
- Podemos intentar tantas preguntas como queramos. Siempre se conservará la puntuación más alta alcanzada.
(*) Esta entrada forma parte del Carnaval de Matemáticas,
que en esta octogésima octava edición,también denominada 11.2,
está organizado por Rafael Martínez González
a través de su blog El mundo de Rafalillo.