Superficies de hojas con GeoGebra
SUPERFICIES DE HOJAS CON GEOGEBRA
Débora Pereiro Carbajo
En clase me gusta proponer pequeños proyectos de investigación con GeoGebra. Este curso, motivada por el proyecto “Miradas de la geometría” (organizado por las asociaciones de matemáticas Agapema y Les Maths en Scene), me propuse trabajar con el alumnado de 1º de ESO: poliedros, cúpulas geodésicas y superficies.
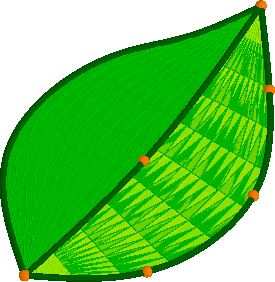
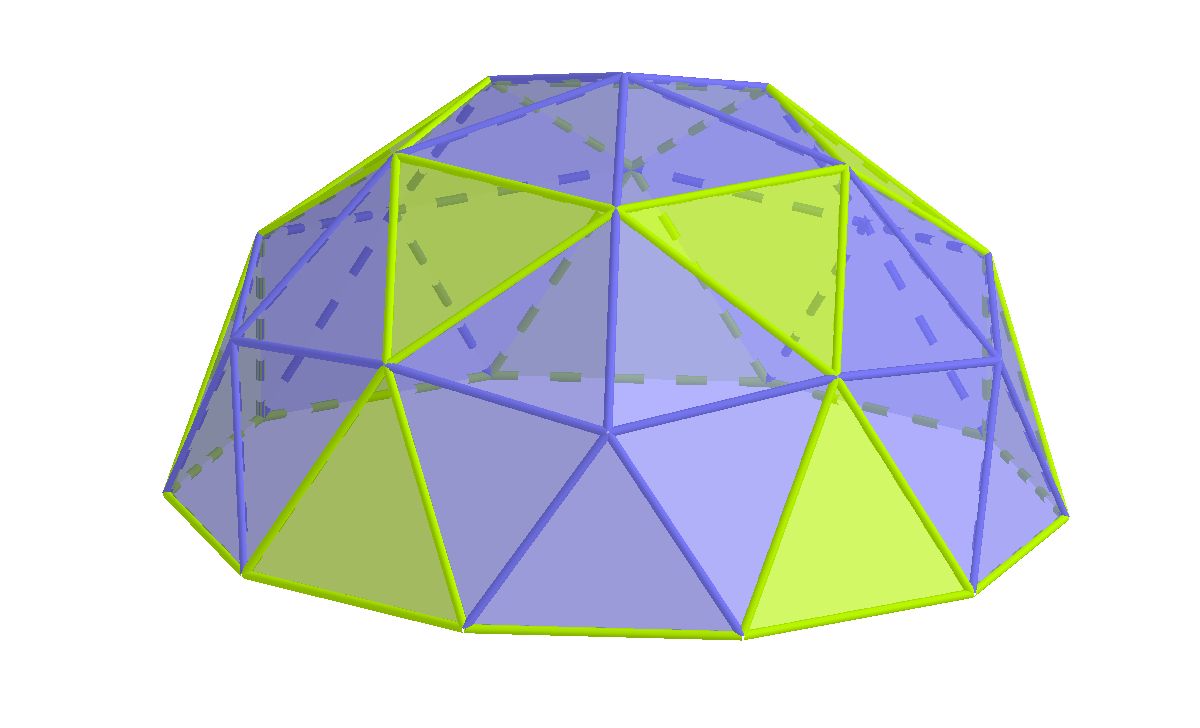
Fig. 1 y 2. Cúpula geodésica y hoja
Puesto que sobre las cúpulas geodésicas ya he hablado (en un artículo publicado en Suma, N.º 93 de Abril 2020) en esta ocasión voy a hacerlo sobre superficies, en concreto sobre las superficies de las hojas de árboles o plantas.